

Next: The membership problem, or
Up: A Mathematical-Algorithmic Approach to
Previous: From an abstract definition
``The automatic computer really forces the precision of thinking
which is alleged to be a product of any study of mathematics," said
George Forsythe in [F]. Indeed,
before proceeding, a very crucial question has to be asked:
Can a computer run our algorithm at all? Obviously, we have to
translate the algorithm into a programming language. But this
will not suffice, and it is not the main point here. We have already
hinted that we may have some problems ``executing" this algorithm.
``If we would have let the algorithm run forever..." we said;
obviously we cannot.
If an algorithm or a computer program runs forever, we unfortunately,
will not be around to see the results.... We don't want it to run
forever. We want it to get some input, run for a finite amount of time,
and produce some output, hopefully the desirable output.
If we want our algorithm to be implemented on a computer, we have to
define better the algorithmic problem we want to solve. The set  is an infinite set, but, our algorithm will obviously not
produce an infinite set. This means that we have to define
the finite subset of
is an infinite set, but, our algorithm will obviously not
produce an infinite set. This means that we have to define
the finite subset of 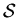 that we want the algorithm to
generate.
This point must be very well clarified in class before proceeding.
Here is the right place to introduce the notion of algorithmic
problem, as we have to define the specific algorithmic problems
we want to solve.
that we want the algorithm to
generate.
This point must be very well clarified in class before proceeding.
Here is the right place to introduce the notion of algorithmic
problem, as we have to define the specific algorithmic problems
we want to solve.
The notion of algorithmic problems, a term coined by Harel [H], is a very important one in the field of
computer science. If the students are not yet familiar with this notion,
it is recommended to devote some time and effort on this issue.
We only very briefly mention that an algorithmic problem consists of: A
characterization of a legal, possibly infinite, collection of
potential input sets, and a specification of the desired outputs as a
function of the inputs. The solution to an algorithmic
problem is an algorithm, which when executed on a legal input set, is
expected to produce the output as required.
Back to our problem then. We can easily find out that
there are several appropriate algorithmic problems that we can
formulate. Here are two examples:
Example 1: Given an integer 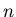 , generate all the elements of
, generate all the elements of
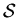 defined by axioms A1-A3, that are smaller than
defined by axioms A1-A3, that are smaller than 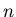 .
.
Example 2: Given an integer 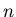 , generate the first
, generate the first 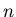 elements
of
elements
of 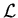 defined by axioms A1-A3.
defined by axioms A1-A3.
One way of solving the problem given in the first example, is generating
the first elements
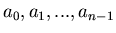 , noticing that
, noticing that 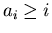 ;
then throwing away elements that are greater than
;
then throwing away elements that are greater than 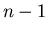 . This is a generation problem which leads to Example 2.
. This is a generation problem which leads to Example 2.
Another way of solving the problem of the first example is
asking if each integer 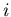 ,
, 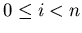 ,
belongs to
,
belongs to  . This leads to the membership problem
which we will discuss in the next section.
. This leads to the membership problem
which we will discuss in the next section.


Next: The membership problem, or
Up: A Mathematical-Algorithmic Approach to
Previous: From an abstract definition
2004-01-05