

Next: Summary
Up: A Mathematical-Algorithmic Approach to
Previous: The membership problem, or
To conclude we would like to present an algorithm for
the generation of the first 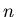 elements of
elements of 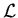 ,
which is based on a recursive definition of
,
which is based on a recursive definition of
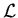 . The the algorithm itself is not recursive. The
teacher should not fail to use this opportunity and point out the
difference between a recursive definition of a concept and a recursive
algorithm. Claim 4, which has to be proven mathematically (in
class or as a home exercise), defines
. The the algorithm itself is not recursive. The
teacher should not fail to use this opportunity and point out the
difference between a recursive definition of a concept and a recursive
algorithm. Claim 4, which has to be proven mathematically (in
class or as a home exercise), defines 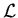 recursively.
recursively.
Claim 4:
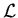 can be defined as follows:
can be defined as follows:
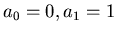 , and for every
, and for every 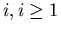 ,
,
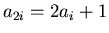 ,
,
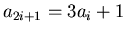 .
.
Below is the algorithm given as a Pascal program
which outputs all the elements of  from
from  to
to 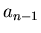 :
:
program  (input,output);
(input,output);
const n = 10000;
var i: integer;
a: array[0..n] of integer;
begin
a[0]:=0; a[1]:=1;
for i:=1 to (n-1) div 2 do
begin
a[2 i]:=2
i]:=2 a[i]+1;
a[i]+1;
a[2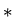 i+1]:=3
i+1]:=3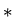 a[i]+1
a[i]+1
end;
for i:=0 to n-1 do write(a[i])
end.
As mentioned before we can now solve the problem of Example1
formulated in the previous section. To solve this problem it is
sufficient to generate the elements ![$a[0]$](img59.png) to
to ![$a[n-1]$](img60.png) , and ignore
the elements that are greater than
, and ignore
the elements that are greater than 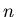 .
.


Next: Summary
Up: A Mathematical-Algorithmic Approach to
Previous: The membership problem, or
2004-01-05
(input,output);
i]:=2
a[i]+1;
i+1]:=3
a[i]+1