

Next: Bibliography
Up: A Mathematical-Algorithmic Approach to
Previous: The generation problem -
The aim of this work was to show by means of a case study how
algorithmic thinking and mathematical thinking can be integrated in high school or
college curriculum. The idea is to introduce a subject into the
mathematics or the computer science curricula, and to then discuss
it in a way that leads to small research questions, and encourages
the algorithmic approach.
From the computer science and mathematics curricula we discussed
topics like algorithmic problems, and algorithms, decision problems and
recursion, and touched upon issues like the correctness of
algorithms, and data structures. However, we did not expect
to cover or complete in any way all the aspects of the given example,
or the issues we mentioned or pointed out for discussion.
There are many more questions to be discussed, which may lead to interesting
``mathematical discoveries" made by the students, and may serve as an
opening to more profound theoretical issues.
We can ask for example: What happens if we change the three axioms to:
A1. 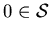 ,
,
A2.
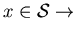
 and
and
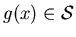 ,
,
A3. 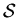 is the minimal set satisfying A1 and A2.
is the minimal set satisfying A1 and A2.
This will lead to the more complicated topics of computer science
and mathematics, asking what if 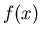 and
and 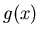 are
computable, and what if they are not.
are
computable, and what if they are not.
There are more profound issues that can be discussed. We mentioned the
complexity and correctness of algorithms, but we did not go into
detail, not even analyzing the complexity of the algorithms we
presented. However as we mentioned above, we definitely
prepared the ground for further study of these subjects,
in a later stage of the students learning.
It should be emphasized, however, that even presenting in detail
only what we have in this paper, might constitute a crucial contribution
to the students' mathematical education as a well-established
basis for further studies. It might not be suitable for the entire
student population of high schools and colleges; it was not meant to.
It was designed for students with a greater and deeper interest
in mathematics and computer science, or in logical thinking.
We are sure that the students who have a strong interest in mathematics
will find this example most attractive.
Acknowledgment
We wish to thank our colleague A. Arcavi with whom we had very
stimulating and fruitful discussions.


Next: Bibliography
Up: A Mathematical-Algorithmic Approach to
Previous: The generation problem -
2004-01-05